In this technical literature we have described and discussed various micro nano bubble properties taking various references from articles and technical papers along with some practical data. But basically, to understand this novel technology first of all we need to understand basic fundamentals of micro and nano bubbles, their generation and their properties.
Now we will list the basic characteristics of micro nano bubbles and will try to understand its fundamentals.
- Small bubble size: –
The size of MBs (micro bubbles) is generally μm order; it depends on the working field, that is, 10–40 μm for bio-activity field and less than 100 μm for fluid physics field. While less than 10 μm are found to be very vast applications in different fields like water and waste water treatment, aeration, chemical reaction. While bubbles size less than 1 μm are useful in the field of analytical science, nano technology, targeted drug delivery system in medical science etc.
- Extremely Slow rising velocity –
The rising velocity of an MB depends on the physical properties of liquids. For MBs of 100 μm diameter, Re number (=dUρ/μ) is nearly 1, and its shape is spherical. Such MBs behave as fluid (clean) spheres or solid (unclean) spheres. By the experimental results of the MBs’ rising velocity, both fluid and solid spherical behaviors were observed, while the rather many experimental results following the Stokes equation.
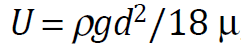
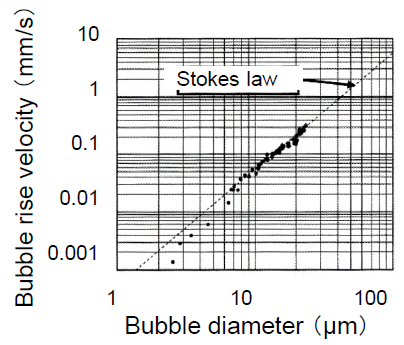
where U is the rising velocity, ρ is the liquid density, g is the gravitational acceleration, d is the bubble diameter and μ is the liquid viscosity. For example, 10 μm MBs rise only 20 cm in 1 h.
- Decreasing Friction Drag –
Friction drag of gas–liquid two-phase flow decreases with increasing MB volume fraction in vertical pipe flow.
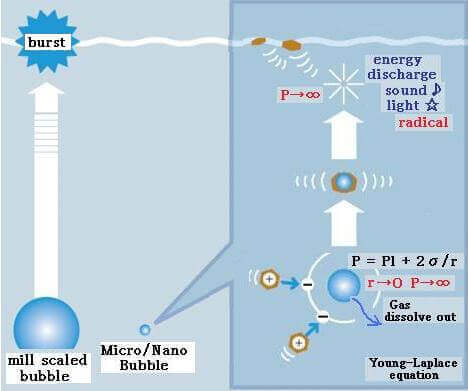
- High Pressure inside Micro Nano Bubbles –
Using Young–Laplace equation, the pressure in a bubble (ΔP) whose diameter is d increases to that larger than the surrounding pressure due to the surface tension σ.
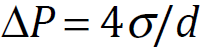
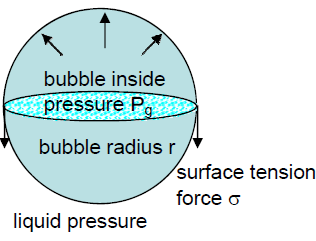
For example, the inner pressures of bubbles whose diameters are 1 μm and 100 nm are 3.87 and 29.7 atm, respectively, (surface tension of water at 20°C: 72.8 mN/m, the surrounding pressure of bubble is 1 atm). With decreasing bubble size, the pressure in the bubble increases. With decreasing bubble size, the partial pressure of dissolved gas component, that is, the driving force of dissolution, increases and the gas dissolves easily.
- Large interfacial Area –
Interfacial area of bubbles divided by volume A/V is obtained by following equation with decreasing bubble diameter d, A/V increases and contributes to gas dissolution fraction.
![]()
- Large Gas Dissolution –
Mass transfer rate from gas to liquid, or dissolving rate N (mol/s), is written by following equation when the gas phase mass transfer resistance is neglected.
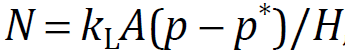
where kL is the liquid phase mass transfer coefficient (m/s), A is the bubble surface area (m2), p is the partial pressure of dissolved component in bubble (Pa), p* is the partial pressure of gas phase equilibrium with dissolved component in liquid (Pa) and H is the Henry constant (p = HC).
The liquid phase mass transfer coefficient kL is written by following equation when Re < 1, and the rising velocity of spherical bubble follows Stokes law, where DL is the gas diffusion coefficient in liquid phase, d is the bubble diameter and U is the bubble rising velocity.
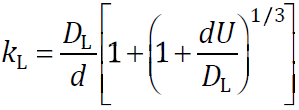
When bubble diameter changes from 1 μm to 1 mm for oxygen–water system (oxygen diffusion coefficient DL = 2.60 × 10–9 m2/s in water), the liquid phase mass transfer coefficient kL becomes 10−4–10−3 m/s by above equation. Mass transfer rate N is obtained by mass transfer equation using the data of kL and bubble inner pressure. When a 1 mm bubble segregates into bubbles whose diameters are 10 μm and 100 nm, bubble numbers increase by 106 and 1012 times, respectively. When the surface area of the 1 mm bubble is defined as 1, the surface areas of 10 μm and 100 nm bubbles increase to 6 × 104 and 6 × 1010, respectively. When the mass transfer rate of the 1 mm bubble during 1 mm rise is considered as 1, mass transfer rates of 10 μm and 100 nm bubbles become 108 and 1018, respectively, due to the decrease in rising velocity. By using MBs, the dissolution rate increases rapidly.
- Dissolution & Contraction of Micro Nano Bubbles –
Ohnari describes the contraction of MB as follows: For the swirling-type MB generator, the pressure at gas suction becomes 0.06 MPa less than the atmospheric pressure. MBs are formed under the combined pressure of atmospheric pressure and static pressure; they are pressurized by liquid and begin to contract. Due to high pressure and high temperature, contraction and dissolution of MBs take place. A 20 μm MB contracts and under 10 μm, it contacts rapidly and disappears. On the other hand, MBs larger than 65 μm will expand further.
- Negatively Charged Surface of Micro Nano Bubbles (-ve Zeta Potential) –
Takahashi measured the surface potentials of MBs using the experimental set-up of electrophoresis cells shown in following figures. MBs formed by the generator in the water reservoir were introduced to the electrophoresis cell (1.0 mm thick, 23.0 mm high and 75.0 mm wide). A transfer switch was used to change the direction of the electric potential in the electrophoresis cell every 1 s. As MBs are charged negatively, MBs rise in a zigzag manner as shown in following figures.
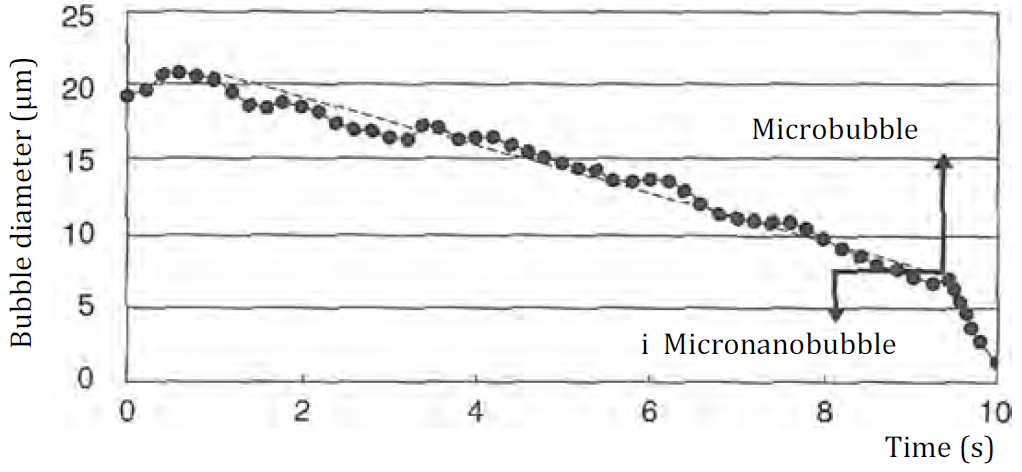
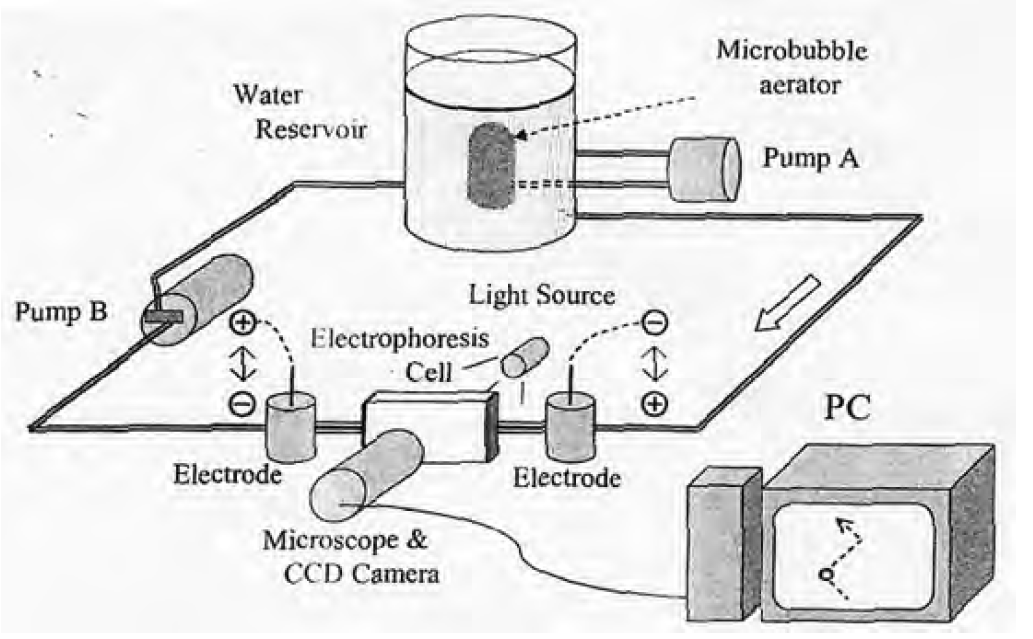
By measuring the vertical rising velocity of MBs, the bubble size is obtained using Stokes equation, and from the horizontal velocity, the ζ potential of MBs is obtained using following Smoluchowski equation
![]()
where ζ is the zeta potential (V), μ is the viscosity of water (kg/ms), u is the mobility (m2/sV) and ε is the permittivity of water (s2C2/kgm3).